Question

A 0.060 kg ball hits the ground with a speed of –32 m/s. the ball is in contact with the ground for 45 milliseconds and the ground exerts a 55 n force on the ball. what is the magnitude of the velocity after it hits the ground? 9.3 m/s 12 m/s 41 m/s 73 m/s

Answer 1

(A)

Step-by-step explanation:

I took the test

Answer 2

Approximately
`9.3\; {\rm m\cdot s^(-1)}`.

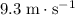Step-by-step explanation:

Apply unit conversion:

`t = 45\; {\rm ms} = 45 * 10^(-3)\; {\rm s}`.

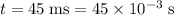At a velocity of
`v`, the momentum
`p` of an object of mass
`m` would be
`p = m\, v`.

Initial momentum of this ball:

`\begin{aligned}p_(0) &= m\, v_(0) \\ &= 0.060\; {\rm kg} * (-32\; {\rm m\cdot s^(-1)}) \\ &= (-1.92\; {\rm kg \cdot m \cdot s^(-1)})\end{aligned}`.

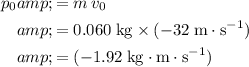When a constant force
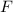`F` is exerted on an object for a duration of length
`t`, the impulse
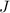`J` applied to that object would be
`J = F\, t`.

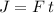Impulse that the ground applied to this ball:

`\begin{aligned}J &= F\, t \\ &= 55\; {\rm N} * (45 * 10^(-3)\; {\rm s}) \\ &= 2.475\; {\rm N \cdot s}\end{aligned}`.

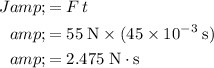Note that
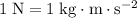`1\; {\rm N} = 1\; {\rm kg \cdot m \cdot s^(-2)}`. Thus, the impulse applied to this ball would be equivalent to:

`\begin{aligned}J &= 2.475\; {\rm (kg \cdot m \cdot s^(-2)) \cdot s} \\ &= 2.475\; {\rm kg \cdot m \cdot s^(-1)}\end{aligned}`.

After this impulse was applied, the momentum of this ball would become:

`\begin{aligned}p_(1) &= p_(0) + J \\ &= (-1.92\; {\rm kg \cdot m \cdot s^(-1)}) + 2.475\; {\rm kg \cdot m \cdot s^(-1)} \\ &= 0.555\; {\rm kg \cdot m \cdot s^(-1)}\end{aligned}`.

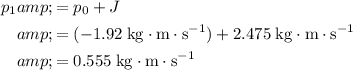The new velocity of this ball would be:

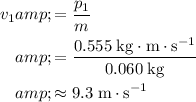`\begin{aligned}v_(1) &= (p_(1))/(m) \\ &= \frac{0.555\; {\rm kg \cdot m \cdot s^(-1)}}{0.060\; {\rm kg}} \\ &\approx 9.3\; {\rm m\cdot s^(-1)}\end{aligned}`.