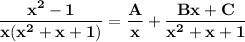Answer:
A.
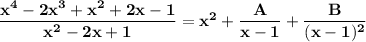
B.
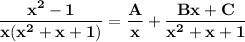
Explanation:
A.
Given that:
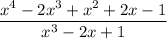
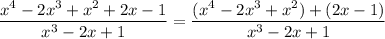
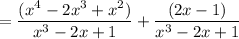
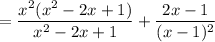
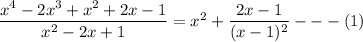
Further, the partial fraction decomposition of
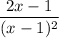 can be written as:
can be written as:
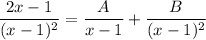
From equation one, replacing the values; we have the partial fraction decomposition of the function to be:
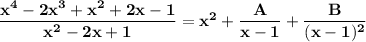
B.
Given that:
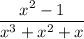
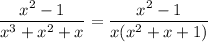
Therefore, the partial fraction of decomposition is: