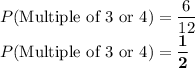Question

There is a spinner with 12 equal areas, numbered 1 through 12.. If the spinner is spun once, what is the probability that the result is a multiple of 3 or a multiple of 4

Answer 1

`(1)/(2)`

Explanation:

Given that, spinner has 12 equal areas, so there are 12 possibilities of occurrences i.e. {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

Multiples of 3 are: {3, 6, 9, 12}

Multiples of 4 are: {4, 8, 12}

To find the multiple of 3 or 4, we need to find the union of the above two sets.

Multiples of 3 or 4: {3, 4, 6, 8, 9, 12}

Number of multiples of 3 or 4 = 6

Formula for probability of an event E can be observed as:

`P(E) = \frac{\text{Number of favorable cases}}{\text {Total number of cases}}`

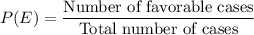
Here, number of favorable cases are 6 and

Total number of cases are 12.

Therefore the required probability is:

`P(\text{Multiple of 3 or 4}) = (6)/(12)\\P(\text{Multiple of 3 or 4}) = \bold{(1)/(2)}`