Question

A pendulum is transported from sea-level, where the acceleration due to gravity g = 9.80 m/s2, to the bottom of Death Valley. At this location, the period of the pendulum is decreased by 5.00%

Answer 1

`g'=10.78\ m/s^2`

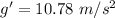
Step-by-step explanation:

The time period of a simple pendulum is given by :

`T=2\pi \sqrt{(L)/(g)}`

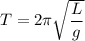
L is length of the pendulum and g is acceleration due to gravity

At the bottom of Death valley, g = 9.8 m/s²

We need to find the value of g if the period of the pendulum is decreased by 5.00%.

T'=(T-0.05T)= 0.95 T

`T\propto (1)/(√(g) )\\\\(T)/(T')=\sqrt{(g')/(g)}\\\\(T)/(0.95T)=\sqrt{(g')/(9.8)}\\\\(1)/(0.95)=\sqrt{(g')/(9.8)}\\\\1.1=(g')/(9.8)\\\\g'=10.78\ m/s^2`

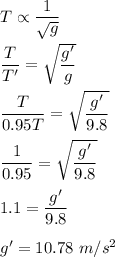
So, the new value of acceleration due to gravity is
`10.78\ m/s^2`.