Question

A bullet is fired straight up from a gun with initial velocity 1120 feet per second at an initial height of 8 feet. Use the formula h = − 16 t 2 + v 0 t + 8 to determine how many seconds it will take for the bullet to hit the ground. (That is, when will h = 0 ?) Round your answer to 2 decimal places

Answer 1

70 seconds

Explanation:

Given that;

The initial velocity
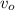`v_o` of the bullet fired = 1120 ft/s

Initial height h = 8 feet

The expression to determine how many seconds it takes the bullet to hit the ground is:

`h = -16t^2 +v_ot + 8`

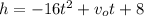
Thus;

Replacing the value of
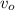`v_o` = 1120 and h = 0 (i.e. when h =0) in the above expression; we have:

`0= -16t^2 +(1120)t + 8`

`= -16t^2 +(1120)t + (8-0)`

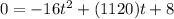
= -16t² + 1120t + 8

mulitiply through by (-)

= 16t² -1120t - 8

Divide through by 8

= 2t² - 140t - 1

The above expression forms a quadratic equation.

where;

a = 2

b = -140

c = - 1

So, by using the quadratic formula
`(-b \pm √(b^2-4ac))/(2a)`, we have:

`= (-(-140) \pm √((-140)^2-4(2)(-1)))/(2(2))`

`= (140 \pm √(19600-(-8)))/(4)`

`= (140 \pm √(19608))/(4)`

`= (140 \pm 140)/(4)`

`=(140+ 140)/(4) \ \ \ OR \ \ \ (140-140)/(4)`

`=(280)/(4) \ \ \ OR \ \ \ 0`

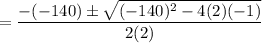
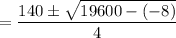
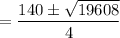
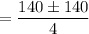
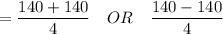
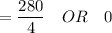
= 70

Thus, the time (in seconds) it took the bullet to it the ground = 70 seconds