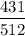Solution :
Let us consider the squares be
![$[1, 16] * [16, 32]$](https://img.qammunity.org/2021/formulas/mathematics/college/232wekxi4xaoqdqu1nbgwtvzmj8lkh8y2r.png)
If x ranges from the 0 to 16 and the y ranges from 16 to 32, we see that the boundary of the region
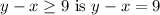 which goes from the
which goes from the
 .
.
And so it is easier to find the area of region where
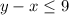 . This is the triangle with points
. This is the triangle with points
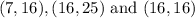 as its vertices.
as its vertices.
The area if the triangle is =
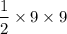
=
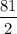
Now the entire area is
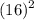 = 256
= 256
Then,
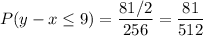
or
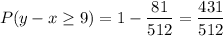
Thus the answer is