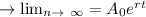Question

If an initial amount A0 of money is invested at an interest rate i compounded times a year, the value of the investment after t years is If we let n = 8, that is referred to as the continuous compounding of interest. Use L' Hospital's Rule to show that if interest is compounded continuously, then the amount after years is A=A0eit

Answer 1

Following are the solution to the given point:

Explanation:

Please find the comp[lete question in the attached file.

Given:

`\bold{ \lim_(n \to \ \infty) (1+ (r)/(n))^(nt) =e^(rt)}`

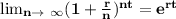
In point 1:

`\to y = (1+ (r)/(n))^(nt)`

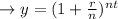
In point 2:

`\to \ln (y)= nt \ln(1+ (r)/(n))`

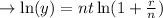
In point 3:

Its key thing to understand, which would be that you consider the limit n to
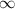`\infty`, in which r and t were constants!

`=lim_(n \to \ \infty) \ln (y) = lim_(n \to \ \infty) nt \ln(1+(r)/(n))\\\\= lim_(n \to \ \infty) (\ln(1+(r)/(n)))/((1)/(nt))\\\\= lim_(n \to \ \infty) ((-r)/((n^2)/((1+(r)/(n)))))/(- (1)/(n^2t))\\\\= lim_(n \to \ \infty) ((rn^2t)/(n^2))/((1+(r)/(n)))\\\\= lim_(n \to \ \infty) (rt)/((1+(r)/(n)))\\\\= (rt)/((1+(r)/(0)))\\\\=rt`

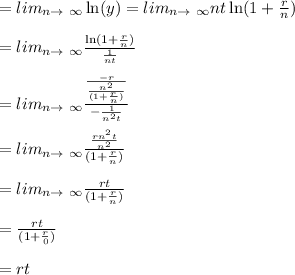
In point 4:

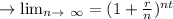`\to \lim_(n \to \ \infty) = (1+(r)/(n))^(nt)` and

`\to \lim_(n \to \ \infty) = A_0e^(rt)`