Question

Los satélites de televisión giran alrededor de la Tierra en una órbita de 42370 km de radio. a) ¿Cuánto vale la aceleración de la gravedad en esa órbita? (Resultado: g = 0,22 m/s2 ) b) ¿Cuánto pesará allí un satélite de 1200 kg? (Resultado: P = 264 N) Datos: G = 6,67 10-11 Nm2 /kg masa de la Tierra: 6 1024 kg

Answer 1

(a) La aceleración de la gravedad en esa órbita es 0.22
`(m)/(s^(2) )`

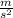
(b) Un satélite de 1,200 kg pesará allí 264 N.

Step-by-step explanation:

(a) Cada punto del espacio tiene un valor del campo proporcional a la función, siguiendo el modelo de gravitación de Newton:

`g=G*(m)/(r^(2) )`

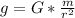
donde m será masa, r la distancia entre los objetos y G la constante de gravitación universal, cuyo valor es
`G=6.672*10^(-11)(N*m^(2) )/(kg )`

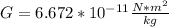
En este caso:

• m= 6*10²⁴ kg
• r=42,370 km= 42,370,000 m

Reemplazando:

`g=6.672*10^(-11)(N*m^(2) )/(kg )*(6*10^(24)kg )/((42,370,000 m)^(2) )`

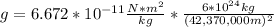
Resolviendo, obtenes:

g= 0.22
`(m)/(s^(2) )`

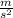
La aceleración de la gravedad en esa órbita es 0.22
`(m)/(s^(2) )`

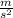
(b) La ley fundamental de la dinámica o segunda ley de Newton expresa que la fuerza neta que es aplicada sobre un cuerpo es proporcional a la aceleración que adquiere en su trayectoria. Esto se expresa matemáticamente como:

F= m*a

en donde F es fuerza neta , m la masa y a la aceleración.

El peso es la fuerza que ejerce la gravedad sobre una masa, por lo que se obtiene de manera análoga a la fuerza:

P=m*g

En este caso la masa m tiene un valor de 1,200 kg y la gravedad g un valor de 0.22
`(m)/(s^(2) )`.

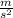Reemplazando:

P=1,200 kg*0.22
`(m)/(s^(2) )`

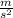
Resolviendo:

P= 264 N

Un satélite de 1,200 kg pesará allí 264 N.