Question

The head of maintenance at XYZ Rent-A-Car believes that the mean number of miles between services is 4959 miles, with a standard deviation of 448.If he is correct, what is the probability that the mean of a sample of 43 cars would differ from the population mean by less than111 miles? Round your answer to four decimal places.

Answer 1

0.8958

Explanation:

Given that:

The mean
`\mu` = 4959

The standard deviation
`\sigma` = 448

The sample size n = 43

`\mu_(\overline x) = \mu = 4959`

`\sigma __(\overline x)} = (\sigma)/(√(n))= (448)/(√(43))`

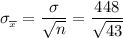
By applying the central limit theorem;

`\overline X \sim N \bigg( \mu_(\overline x) = 4959 , \sigma_(\overline x) = (448)/(√(43))\bigg )`

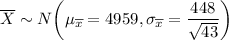
The purpose of this question is to calculate the probability that the mean of a sample of 43 cars would differ from the population mean by less than111 miles.

This implies that;

`P( |\mu-\overline x| <111) = p( 4959-111 < \overline X < 4959 +111)`

`= P( 4848 < \overline X < 5070)`

`= P \bigg ( ( \overline x - \mu_x )/( (\sigma)/(√(n))) < Z < ( \overline x - \mu_x )/( (\sigma)/(√(n))) \bigg )`

`= P \bigg ( (4848 -4959 )/( (448)/(√(43))) < Z < (5070 -4959 )/( (448)/(√(43))) \bigg )`

`= P \bigg ( (-111 )/( 68.319) < Z < (111 )/(68.319) \bigg )`

`= P ( -1.6247< Z < 1.6247 )`

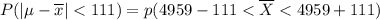
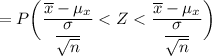
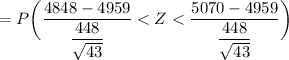
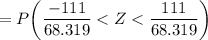
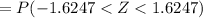
= P ( Z < 1.627 ) - P(Z < -1.627)

From the standard normal tables

= 0.94791 -0.05208

= 0.89583

≅ 0.8958 to four decimal places.