Given :
A solid object is dropped into a pond with a temperature of 20 degrees Celsius.
The function f(t) = Ce(-kt) + 20 represents the situation where t is time in minutes, C is a constant and k = 0.0399.
To Find :
The initial temperature of the object.
Solution :
Putting t = 4 in given equation, we get :
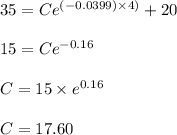
Putting value of C in given equation, we get :
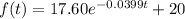
Now, for initial temperature is given at t=0 s .
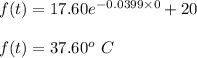
Therefore, the initial temperature of the object is 37.60° C.
Hence, this is the required solution.