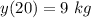Answer:
a
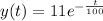
b
Explanation:
From the question we are told that
The volume of brine in the tank is
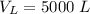
The mass of the salt is
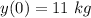
The rate at which water enters that tank is
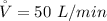
Generally the rate at which salt enters the tank is mathematically represented as
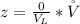
=>
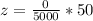
Here the zero implies that there is no salt entering the tank
Generally the rate at which salt leaves the tank is mathematically represented as
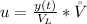
=>
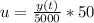
=>
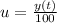
Generally the rate of salt flow in and out of the tank is
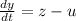
=>
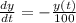
=>
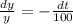
=>
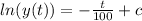
at time t = 0 y(0) = 11
=>
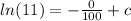
=>
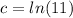
So
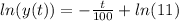
taking exponent of both sides
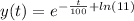
=>
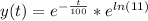
=>
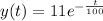
Generally at t = 20 minutes
The amount of salt in the tank is mathematically represented as
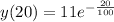
=>