This question is missing some parts. Here is the complete question.
Consider the oriented path which is a straight line segment L running from (0,0) to (16,16).
(a) Calculate the line inetrgal of the vector field F = (3x-y)i + xj along line L using the parameterization B(t) = (2t,2t), 0 ≤ t ≤ 8.
Enter an exact answer.

(b) Consider the line integral of the vector field F = (3x-y)i + xj along L using the parameterization C(t) =
 , 16 ≤ t ≤ 32.
, 16 ≤ t ≤ 32.
The line integral calculated in (a) is ____________ the line integral of the parameterization given in (b).
Answer: (a)
 384
384
(b) the same as
Explanation: Line Integral is the integral of a function along a curve. It has many applications in Engineering and Physics.
It is calculated as the following:
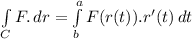
in which (.) is the dot product and r(t) is the given line.
In this question:
(a) F = (3x-y)i + xj
r(t) = B(t) = (2t,2t)
interval [0,8] are the limits of the integral
To calculate the line integral, first substitute the values of x and y for 2t and 2t, respectively or
F(B(t)) = 3(2t)-2ti + 2tj
F(B(t)) = 4ti + 2tj
Second, first derivative of B(t):
B'(t) = (2,2)
Then, dot product between F(B(t)) and B'(t):
F(B(t))·B'(t) = 4t(2) + 8t(2)
F(B(t))·B'(t) = 12t
Now, line integral will be:
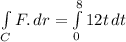
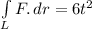
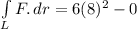
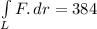
Line integral for the conditions in (a) is 384
(b) same function but parameterization is C(t) =
 :
:
F(C(t)) =
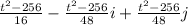
F(C(t)) =

C'(t) =
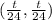
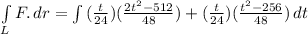


Limits are 16 and 32, so line integral will be:
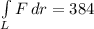
With the same function but different parameterization, line integral is the same.