Question

The accompanying data resulted from a flammability study in which specimens of four different fabrics were tested to determine burn times. Fabric Type Ýi. Si ni 1 11.6 .75 42 13.1 .88 43 14.5 .94 44 15.6 .98 4The analysis of variance is given as follows: Source DF SS MS F p-value Fabric Type 3 28.322 9.441 11.875 0.002 Error 12 9.543 0.795 Total 15 37.865 A) Write a linear contrast for Question 1: Is the mean burn time of fabrics of type 3 different than the mean burn time of type 4? B) Write a linear contrast for Question 2: Is the mean burn time of fabrics of type 1 different than the average of burn times of fabrics of the other three types (2, 3, 4)? C) Are the two contrasts defined in (a) and (b) mutually orthogonal? Explain why or why not. D) Conduct a F test about the linear contrast defined in (a). Use a = 0.05

Answer 1

Following are the solution to the given point.

Explanation:

In point a:

Linear comparison of the mean burning period of textiles of type three different from the mean type 4 burn time:

`\to C_1= \bar{y_3}- \bar{y_4}`

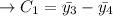
In point b:

Linear comparison to the moderate burning time of type 1 textiles distinct from the average burn periods of all the other three styles of textiles[2,3,4]: is

`\to C_2 = \bar{y_1} - (1)/(3) \bar{Y_2} - (1)/(3) \bar{Y_3} - (1)/(3) \bar{Y_4}`

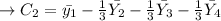
In point c:

The comparison in a and (b) above is orthogonal to one another. Since the number of coefficient products is :

In point d:

The contrast value is
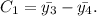`C_1 = \bar{y_3} -\bar{y_4}.` The estimate of the contrast:

`=14.5-15.6\\\\=-1.1`

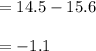
The standard error is

`= \sqrt{0.795 * (2)/(4)}\\\\ = √(0.3975)\\\\= √(0.6305)`

`t= \frac{(\bar{y_3} - \bar{y_4})}{SE(\bar{y_3} - \bar{y_4})}= (-1.1)/(0.6305)= -1.7447`

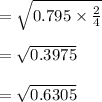
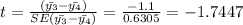
T is 2.1788 as the critical value. Since the value of t=1.7447<th of the critical value is absolute, the null is not rejected

The hypothetical one. theory. Therefore the impact of contrast is not statistically significant.

As we know t is a test F. Alternatively, as we know. The F-statistics at 1,12 df is
`t^2 = -1.7445^2 = 3.0440.`

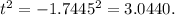
F test is critical to 4,7472.