Answer:
The sample size is

Explanation:
From the question we are told that
The margin of error is
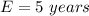
The standard deviation is
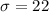
From the question we are told the confidence level is 94% , hence the level of significance is
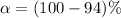
=>
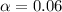
Generally from the normal distribution table the critical value of
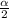 is
is
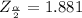
Generally the sample size is mathematically represented as
![n = [\frac{Z_{(\alpha )/(2) } * \sigma }{E} ] ^2](https://img.qammunity.org/2021/formulas/mathematics/college/j63im5d7bkeqfrgf56wd02g4fvud45p15n.png)
=>
![n = [\frac{1.881 } * 22 }{5} ] ^2](https://img.qammunity.org/2021/formulas/mathematics/college/dtx990r65dluls57m0z65fy83tu1qox9u3.png)
=>
