Question

XYZ Inc. has $10 million in excess cash, a market capitalization of $300 million and a market value of debt of $110 million. Its cost of equity is 12% and its cost of debt is 5%. The corporate tax rate is 31%. Calculate the WACC for XYZ Inc. Express your answer in percent and round to two decimals (do not include the %-symbol in your answer).

Answer 1

We know,

`$\text{WACC}=\text{equity weightage } * \text{equity cost} + \text{net debt weightage} * \text{debt cost} * (1 -\text{tax rate})$`

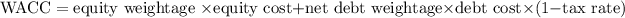
Net debt = debt market value - excess cash

= 110 - 10

= 100 million dollar

`$\text{net debt weightage}=\frac{\text{market value of net debt}}{\text{equity market value+ net debt market value}}$`

`$=(100)/(300+100)$`

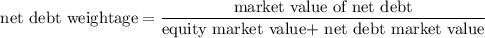
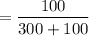
= 0.25

`$\text{equity weightage}=\frac{\text{market value of equity}}{\text{equity market value+ net debt market value}}$`

`$=(300)/(300+100)$`

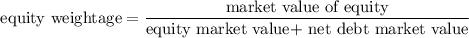
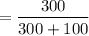
= 0.75

Therefore, WACC = 0.75 x 12% + 0.25 x 5% x (1 - 31%)

= 0.75 x 12% + 0.25 x 5% x (1 - 0.31)

= 0.75 x 12% + 0.25 x 5% x 0.69

= 9% + 0.862%

= 9.862%