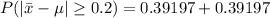Question

If a random sample of 47 steel bolts is selected, what is the probability that the sample mean would differ from the population mean by more than 0.2 millimeters?

Answer 1

Complete Question

Thompson and Thompson is a steel bolts manufacturing company. Their current steel bolts have a mean diameter of 143 millimetres, and a standard deviation of 5. If a random sample of 47 steel bolts is selected, what is the probability that the sample mean would differ from the population mean by more than 0.2 millimetres? Round your answer to four decimal places.

Answer:

The probability is
`P(|\= x - \mu | \ge 0.2 ) = 0.78394`

Explanation:

From the question we are told that

The sample size is n = 47

The mean diameter is
`\mu = 143`

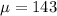
The standard deviation is
`\sigma = 5`

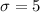
Generally the standard error of the mean is mathematically represented as

`\sigma_(x) = (\sigma )/(√(n) )`

=>
`\sigma_(x) = (5 )/(√(47) )`

=>
`\sigma_(x) = 0.7293`

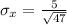
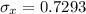
Generally the probability that the sample mean will differ from the population mean by more than 0.2 milli meters is mathematically represented as

`P(|\= x - \mu | \ge 0.2 ) = P((|\= x - \mu|)/(\sigma_(x)) \ge (0.2)/(0.7293) )`

`(|\= x - \mu | -\mu)/(\sigma )  =  |Z| (The  \ standardized \  value\  of  \ {|\= x - \mu |  )`

=>
`P(|\= x - \mu | \ge 0.2 ) = P(|Z| \ge 0.2742 )`

=>
`P(|\= x - \mu | \ge 0.2 ) = P(Z < - 2742) + P(Z > 0.2742)`

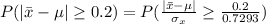
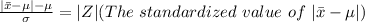
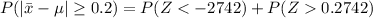
From the z table the area under the normal curve to the left corresponding to -2.742 is

`P(Z < -0.2742) =0.39197`

From the z table the area under the normal curve to the right corresponding to 2.742 is

P(Z > 0.2742) = 0.39197

So

`P(|\= x - \mu | \ge 0.2 ) = 0.39197 + 0.39197`

`P(|\= x - \mu | \ge 0.2 ) = 0.78394`