Question

A distribution of values is normal with a mean of 114.5 and a standard deviation of 23.

Find P47, which is the score separating the bottom 47% from the top 53%.
P47 =
Enter your answer as a number accurate to 1 decimal place. Answers obtained using exact z-scores or z-scores rounded to 3 decimal places are accepted.

Answer 1

The score separating the bottom 47% from the top 53% is 112.8

Explanation:

Let X denote the random variable whose values are normal with a mean of 114.5 and a standard deviation of 23.

Compute the 47th percentile as follows:

`P(X<x)=0.47\\\\P((X-\mu)/(\sigma)<(x-114.5)/(23))=0.47\\\\P(Z<z)=0.47`

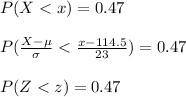
The corresponding z-value is,

z = -0.075

*Use the z-table.

Compute the value of x as follows:

`(x-114.5)/(23)=-0.075\\\\x=114.5-(0.075* 23)\\\\x=112.775\\\\x\approx 112.8`

Thus, the score separating the bottom 47% from the top 53% is 112.8