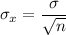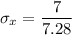Answer:
No, because the Central Limit Theorem posits that regardless of the shape of the underlying population, the sampling distribution of bar x becomes approximately normal as the sample size (n) increases.
The sampling distribution of x is;
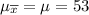
Explanation:
Given that:
The sample size n = 53
The population mean μ = 53
The standard deviation σ = 7
The sampling distribution of x is;
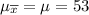
Sampling distribution of the standard deviation is: