Question

A 4.0-kg object is supported by an aluminum wire of length 2.0 m and diameter 2.0 mm. How much will the wire stretch?

Answer 1

The extension of the wire is 0.362 mm.

Step-by-step explanation:

Given;

mass of the object, m = 4.0 kg

length of the aluminum wire, L = 2.0 m

diameter of the wire, d = 2.0 mm

radius of the wire, r = d/2 = 1.0 mm = 0.001 m

The area of the wire is given by;

A = πr²

A = π(0.001)² = 3.142 x 10⁻⁶ m²

The downward force of the object on the wire is given by;

F = mg

F = 4 x 9.8 = 39.2 N

The Young's modulus of aluminum is given by;

`Y = (stress)/(strain)\\\\Y = (F/A)/(e/L)\\\\Y = (FL)/(Ae) \\\\e = (FL)/(AY)`

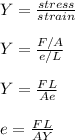
Where;

Young's modulus of elasticity of aluminum = 69 x 10⁹ N/m²

`e = (FL)/(AY) \\\\e = ((39.2)(2))/((3.142*10^(-6))(69*10^9)) \\\\e = 0.000362 \ m\\\\e = 0.362 \ mm`

Therefore, the extension of the wire is 0.362 mm.