Answer:
y = - 4x + 13
Explanation:
In order to do this problem you would need a whole new equation, but you will use what is given to you:
instead of going with:
x - 4y = 20
Turn it into y = mx + b form, also known as slope-intercept form:
x - 4y = 20
-x = -x
_________
- 4y = 20 - x
Then divide both sides by - 4:

You will then get:
y =

From this equation we will only need the slope!
m || =

(This slope is for parallel)
but if you want perpendicular to the slope, then we need the negative reciprocal!
Negative reciprocal is a flipped version of the value that is negative, for example:
2 =
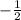
Because
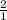 = 2
= 2
Now we will find the perpendicular slope which is:
m ⊥ = - 4
Now substitute this slope into slope intercept form:
y = mx + b
(-3) = -4(4) + b
(Take away parentheses)
-3 = -16 + b
(Move - 3 to the other side, by making it positive, but what you do to one side, you do to the other)
= -13 + 6
(Move - 13 to the other side, by make - 13 into +13)
+13 = +13
________
13 = b
(This is you b, also known as you intercept)
Your answer is:
y = -4x + 13