Question

Heppp asappp plssspppppp

Answer 1

Answer: (6, -1)

=============================================================

Step-by-step explanation:

If you were to multiply both sides of the second equation by 4, then,

`(1)/(2)x-5y = 8\\\\4\left((1)/(2)x-5y\right) = 4*8\\\\2x-20y = 32\\\\`

The original system of equations is equivalent to this system

`\begin{cases}2x+y = 11\\2x-20y = 32\end{cases}`

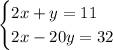
Let's subtract straight down.

• The x terms have the same coefficient (2) out front. This means when we subtract the x terms, they'll go away. 2x-2x = 0x = 0.
• Subtracting the y terms gets us: y-(-20y) = y+20y = 21y
• Subtracting the right hand sides gets us: 11-32 = -21

After those three sets of subtractions are performed, we have this new equation:
`21 y = -21` and that solves to
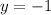`y = -1` (divide both sides by 21).

Now use this y value to find x. You can pick any equation with x & y in it.

`2x+y = 11\\\\2x+(-1) = 11\\\\2x-1 = 11\\\\2x = 11+1\\\\2x = 12\\\\x = 12/2\\\\x = 6`

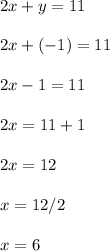
The solution as an ordered pair is (x,y) = (6, -1)

The two lines cross at this location.