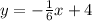Question

Yo can someone help me plz, i would app it

Answer 1

Parallel line - y=6x+9

Perpendicular line - y=-1/6x +4

Explanation:

Parallel lines have a slope that is equal to the origninal equation. You use the y-y1=m(x-x1) equation. In this case, your y1 is 3 and your x1 is -1. Plug these into the equation along with your slope of 6.

y-y1=m(x-x1)

y-3=6(x-(-1))

y-3=6(x+1)

y-3=6x+6 - Distribute

+3 +3 - Add 3 to both sides

y=6x+9

For perpendicular lines, the slope is the negative reciprocal of the given slope. In this case, the slope is -1/6. Your y1 is 4 and your x1 is 0.

y-y1=m(x-x1)

`y - 4 = - (1)/(6) (x - 0)`

Distribute:

`y - 4 = - (1)/(6) x`

+4 +4

Add 4 to both sides:

`y = - (1)/(6) x + 4`