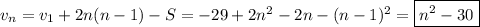If
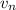 is the n-th term in the sequence, observe that
is the n-th term in the sequence, observe that
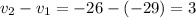

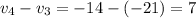
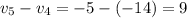
and if the pattern continues,
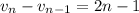
so the sequence is defined recursively by

By this definition,
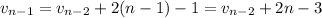
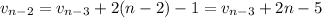
and so on. Then by substitution, we have
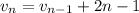
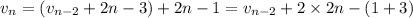
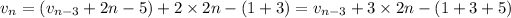
and if we keep doing this we'll eventually get
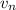 in terms of
in terms of
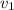 to be
to be
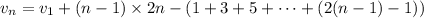
Evaluate the sum:
Let

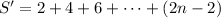
Then
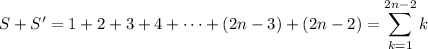
Recall that

so that
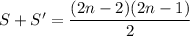
and
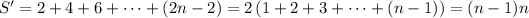
So, we find
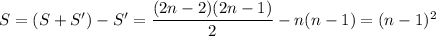
Then the n-th term to the sequence is