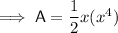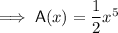Question

Please help me with this.

Answer 1

`\textsf{A}(x)=(1)/(2)x^5`

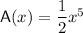
Explanation:

`\textsf{Area of a triangle}=\frac12 * \sf base * height`

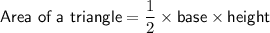
From inspection of the diagram, the base of the triangle is the horizontal line segment between points (0, y) and (x, y). To determine the length of the line segment, find the difference between the x-coordinates of the points:

`\implies \textsf{Base}=x-0=x`

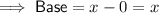
The height of the triangle is the vertical line segment between points (0, 0) and (0, y). To determine the length of the line segment, find the difference between the y-coordinates of the points:

`\implies \textsf{Height}=y-0=y`

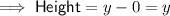
Therefore, substituting these values into the original formula:

`\textsf{Area of a triangle}=(1)/(2)xy`

We have been told that
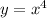`y=x^4`. Substitute this into the found equation so that the Area A of the triangle can be expressed as a function of x:

`\implies \textsf{A}=(1)/(2)x(x^4)`

`\implies \textsf{A}(x)=(1)/(2)x^5`