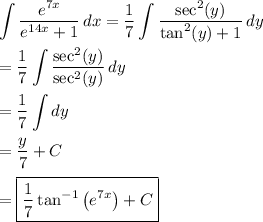a) Substitute
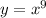 and
and
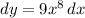 :
:
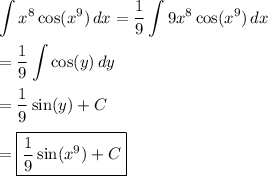
b) Integrate by parts:
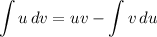
Take
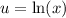 and
and
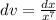 , so that
, so that
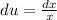 and
and
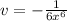 :
:
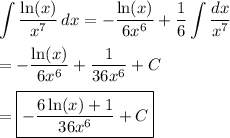
c) Substitute
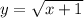 , so that
, so that
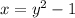 and
and
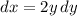 :
:
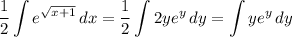
Integrate by parts with
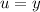 and
and
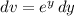 , so
, so
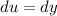 and
and
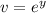 :
:
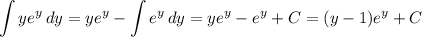
Then
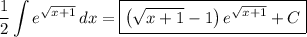
d) Integrate by parts with
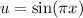 and
and
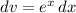 , so
, so
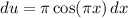 and
and
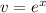 :
:
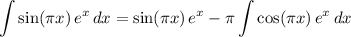
By the fundamental theorem of calculus,
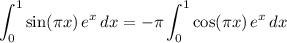
Integrate by parts again, this time with
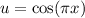 and
and
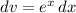 , so
, so
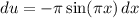 and
and
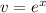 :
:
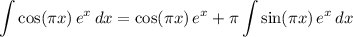
By the FTC,
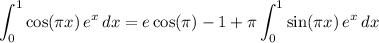
Then
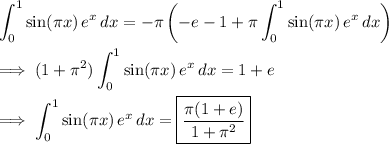
e) Expand the integrand as
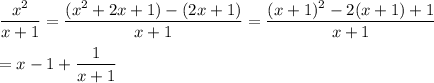
Then by the FTC,
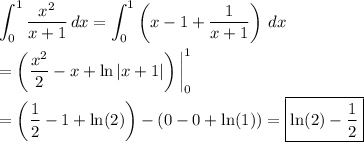
f) Substitute
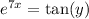 , so
, so
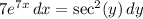 :
: