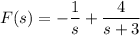6a. By the convolution theorem,

6b. Similarly,
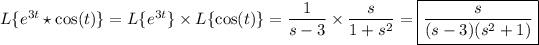
7. Take the Laplace transform of both sides, noting that the integral is the convolution of
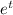 and
and
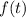 .
.
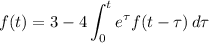
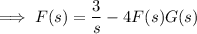
where
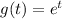 . Then
. Then
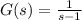 , and
, and

We have the partial fraction decomposition,
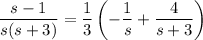
Then we can easily compute the inverse transform to solve for f(t) :