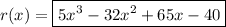Since
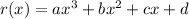 , we have first and second derivatives
, we have first and second derivatives
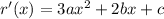
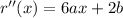
 is supposed to pass through the points C (2, 2) and D (3, 2), so
is supposed to pass through the points C (2, 2) and D (3, 2), so
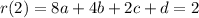
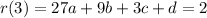
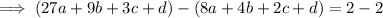

"agreement with
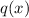 " entails having the same first and second derivatives as
" entails having the same first and second derivatives as
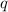 at the point C :
at the point C :
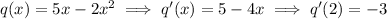
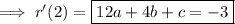
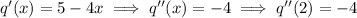
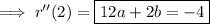
Solve the indicated equations for a, b, and c, and subsequently for d :
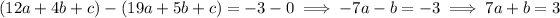
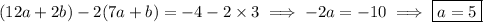
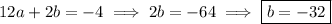
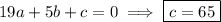
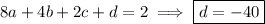
Then the cubic joining C and D is given by