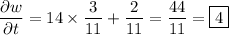a)
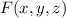 is conservative if it is the gradient field for some scalar function
is conservative if it is the gradient field for some scalar function
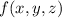 . This would require
. This would require

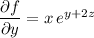
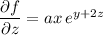
Integrating both sides of the first equation with respect to
 yields
yields
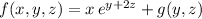
Differentiate with respect to
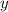 :
:
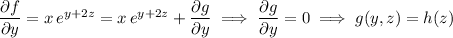
Differentiate with respect to
 :
:
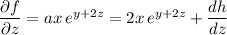
We want
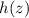 to be independent of
to be independent of
 and
and
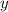 ; we can make them both disappear by picking
; we can make them both disappear by picking
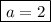 .
.
b) This is the so-called triple product, which has the property
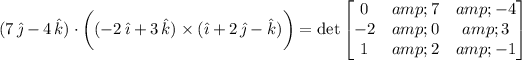
Computing the determinant is easy with a cofactor expansion along the first column:
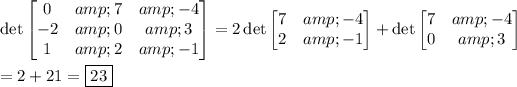
c) Let
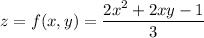
Compute the partial derivatives and evaluate them at
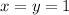 :
:
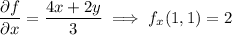
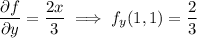
Then the tangent plane to
 at (1, 1, 1) has equation
at (1, 1, 1) has equation
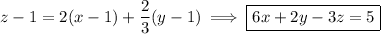
d) In polar coordinates,
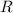 is the set
is the set

Then the integral evaluates to
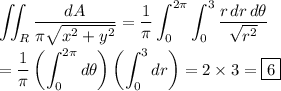
e) By the chain rule,
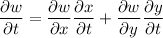
Eliminating the parameter, we find
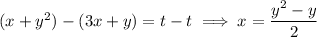
so that
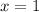 when
when
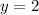 .
.
Compute derivatives:
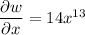

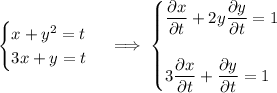
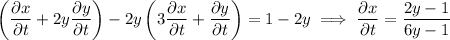
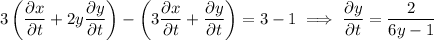
Then at the point (1, 1), the derivative we want is