Answer:
D
Explanation:

The symbol '
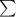 ' , read as sigma, is the symbol for summation. Since the expression below sigma is 'k= 1', while the number above sigma is 3, we are to find the sum of
' , read as sigma, is the symbol for summation. Since the expression below sigma is 'k= 1', while the number above sigma is 3, we are to find the sum of
 with each other from k =1 to k =3.
with each other from k =1 to k =3.
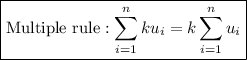

=
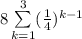 (Applying multiple rule)
(Applying multiple rule)
=
![8[((1)/(4))^(1-1)+((1)/(4))^(2-1)+((1)/(4))^(3-1)]](https://img.qammunity.org/2023/formulas/mathematics/high-school/msxo5pnwnehijmsfz7ppigrmmv9tqpu9ne.png)
=
![8[((1)/(4))^0+((1)/(4))^1+((1)/(4))^2]](https://img.qammunity.org/2023/formulas/mathematics/high-school/e9zdvtn9c67kzs7ywqtsy1ls35wuk4c0kr.png)
=
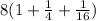
=

=
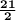
Thus, the answer is D.