Answer:
m = -1/5=-0.20000
Explanation:
1) Find the slope
The slope of a line between two points equals the change in the points' y-coordinates (rise) over the change in their x-coordinates (run).
The coordinates of point 1 are:
 ,
,
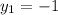
The coordinates of point 2 are:
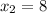 ,
,
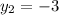
To find the slope, plug the points' x and y-coordinates into the formula and combine to simplify:

- 3 additional steps
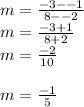
---------
Terms and topics
- Properties of a straight lines
Why learn this
- Whether they are horizontal, vertical, diagonal, parallel, perpendicular, intersecting, or tangent lines, it is a fact of life that straight lines are everywhere. Chances are, you know what a line is, but it is also important to understand their formal definition in order to better understand the various problems that involve them. A line is a one-dimensional figure, with a length but no width, that connects two points. After points, lines are the second smallest building blocks of shapes, which are essential for understanding our world and the spaces we find ourselves in. Additionally, understanding the slope, direction, and behavior of different types of lines is necessary for graphing and understanding certain types of information, an important skill across many industries.