Answer:
C, D
Explanation:
We can solve this graphically and analytically.
Graphically, looking at the attached image below, if we graph the two inequalities and plot the points, you can find the points which are solutions by finding the points in the overlapping area.
This obviously excludes A as it only appears in

C is included as y
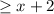 includes the point on the line.
includes the point on the line.
D is obviously a solution.
B is however not a solution because is lies on the line
 , which the inequality excludes.
, which the inequality excludes.
Analytically, if we can find one of the two inequalities where it is not a solution, it is not a solution of the system.
A: (0, 0)
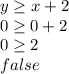
A is not a solution
B: (-2, 2)
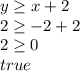
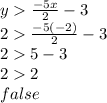
B is not a solution
C: (0, 2)
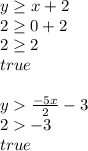
C is a solution
D:
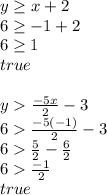
D is a solution