Question

Vertex of gaudratic x2 - 2x -15 (the first 2 is exponent)

Answer 1

• y=x^2-2x-15

x coordinate of vertex

• -b/2a
• -(-2)/2
• 2/2
• 1

y coordinate of vertex

• y=(1)³-2(1)-15
• y=1-2-15
• y=-16

Vertex

• (1,-16)

Answer 2

(1, -16)

Explanation:

Vertex form of a quadratic equation:

`y=a(x-h)^2+k`

where:

• (h, k) is the vertex
• a is some constant

Given equation:

`x^2-2x-15=y`

To convert the given quadratic equation to vertex form, complete the square.

Add 15 to both sides:

`\implies x^2-2x-15+15=y+15`

`\implies x^2-2x=y+15`

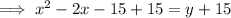
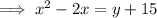
Add the square of half the coefficient of the
`x` term to both sides:

`\implies x^2-2x+\left((-2)/(2)\right)^2=y+15+\left((-2)/(2)\right)^2`

`\implies x^2-2x+1=y+16`

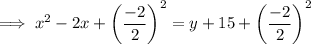
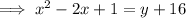
Factor the left side:

`\implies (x-1)^2=y+16`

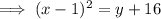
Subtract 16 from both sides:

`\implies (x-1)^2-16=y`

`\implies y=(x-1)^2-16`

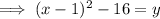
Comparing with the vertex form:

`\implies h=1, \quad k=-16`

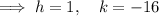
Therefore, the vertex of the given quadratic is (1, -16)