Question

How Va from first equation(5m/s) doesn't equal Va from last equation(4.36m/s)

Answer 1

You get the SAME answer from both equations:

`|V_A|=√(19) \,\,m/s\approx 4.36\,\,m/s`

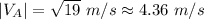
Step-by-step explanation:

Notice that you are dealing with vector equations, and that the first one doesn't give you 5 m/s for the magnitude.

You need to add V0 = 3 (in the x-direction), to

`V_(AO)=2\,cos(60^o)\,\hat i+ 2\,sin(60^o)\,\hat j\\V_(AO)=2\,(1)/(2) cos(60^o)\,\hati + 2\,(√(3) )/(2) \,\hat j\\V_(AO)=1\,\,\hat i + 2\,√(3) \,\hat j`

Therefore, the answer for VA from the first equation is:

`V_A=V_0\,+\,V_(AO)\\V_A=4\,\,\hat i + 2\,√(3) \,\hat j\\|V_A|=√(16+3) =√(19) \approx 4.36\,\,m/s\\\theta = arctan((√(3) )/(4) )\approx 23.41^o`

which is exactly what was calculated in the second approach considering from point C.