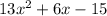Answer:
The area of shaded region is:
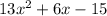
Explanation:
We can see in the diagram that
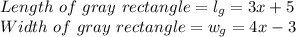
The area of rectangle is given by:
Area = Length * width
Now for gray rectangle
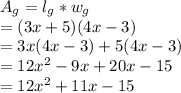
For White Rectangle:
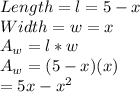
Now,
The area of shaded region will be calculated by subtracting the area of white triangle from the gray triangle.
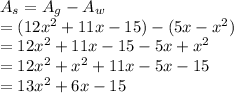
Hence,
The area of shaded region is: