If we evaluate the function at infinity, we get:
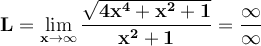
Therefore, being an indeterminate form, we must multiply and divide by the highest degree monomial (x²; remember that we divide the powers of the numerator by 2 since they are inside a square root):

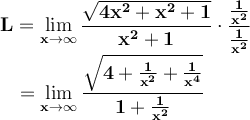
Then, evaluated at infinity, we have:
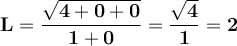
So the limit is 2.