Question

Need help with this. Write an equation that is parallel to the line whose equation is y = −8x − 7?

An equation of the line that has a slope of 3
and a y-intercept of -2 is

Answer 1

Problem 4: y = -8x+b

Problem 5: C: 3x-2

Explanation:

Problem 4:

The given line is in slope intercept form.

The slope-intercept form is:

`y = mx+b`

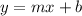
Here the co-efficient of x is the slope of the line. Comparing the given equation with general form

m = -8

Two parallel lines have same slope so the slope of line will be -8.

`y=mx+b\\y = -8x+b`

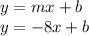
b can be any positive or negative integer as we don't know any point on the line parallel to given line.

Problem 5:

Slope = 3

y-intercept = -2

Slope intercept of line is given by:

`y = mx+b`

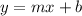
here m is slope and b is y-intercept

Putting the values

`y = 3x-2`

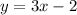
Option C: y=3x-2 is the correct answer

Hence,

Problem 4: y = -8x+b

Problem 5: C: 3x-2