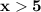Answer:
Solving
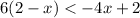 we get
we get
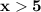
Explanation:
We need to find solution of
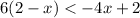
Solving the inequality:
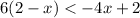
Multiply 6 with terms inside the bracket
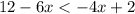
Subtracting 12 on both sides
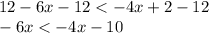
Adding 4x on both sides
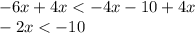
Divide both sides by -2 and the inequality will be reversed i.e < will be changes to >
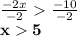
So, after solving
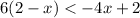 we get
we get