Question

I need the slope and the y - intercept in the equation. I’ll give you a if you help me

Answer 1

• m = slope = 1/2

• The y-intercept = (0, 5)

• The equation of the line is:

`y=(1)/(2)x+5`

Explanation:

Considering the line graph

Some of the points on the line are given by

• (0, 5)

• (2, 6)

• (4, 7)

• (6, 8)

Finding the slop between any two given points

Let us take the point (0, 5) and (2, 6)

`\mathrm{Slope\:between\:two\:points}:\quad \mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(0,\:5\right),\:\left(x_2,\:y_2\right)=\left(2,\:6\right)`

`m=(6-5)/(2-0)`

• 
  `m=(1)/(2)`

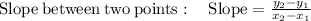
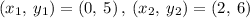
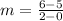
To the y-intercept, set x = 0.

We already know that when x = 0, the value of y = 5

so

• The y-intercept = (0, 5)

Equation of line can be obtained using the point-slope form of the line equation

`y-y_1=m\left(x-x_1\right)`

substituting the values m = 1/2 and any point let say (2, 6)

`y-6=(1)/(2)\left(x-2\right)`

add 6 to both sides

`y-6+6=(1)/(2)\left(x-2\right)+6`

`y=(1)/(2)x+5`

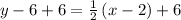
Therefore, the equation of the line is:

• 
  `y=(1)/(2)x+5`