Question

A 1 pF capacitor is connected in parallel with a 2 pF capacitor, the parallel combination then being connected in series with a 3 pF capacitor. The resulting combination is then connected across a battery. Which capacitor has the greatest charge

Answer 1

Hi there!

We can approach this problem in many ways, but to show you how I arrive to the final conclusion, I will begin by solving the circuit with an assigned value for the power source.

Let's use a power source value of 6V (produces nice numbers).

Recall the following rules.

Capacitors in series:

• Voltage ADDS up.
• Charge is EQUAL across each.
• Total capacitance uses the reciprocal rule.

Capacitors in parallel:

• Voltage is EQUAL across each.
• Charge ADDS up.
• Total capacitance is simply the sum.

Solving for total capacitance:

`C_P = 1 + 2 = 3 pF\\\\C_T = (1)/((1)/(3) + (1)/(3)) = 1.5 pF`

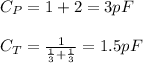
Using rules for capacitors in series and parallel, the total capacitance of the circuit is 1.5 pF.

Thus, the total charge is:

`Q = C_TV\\Q = 1.5 pF * 6 V = 9 pC`

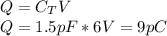
9 pC will go through the parallel combination and the individual capacitor in series with the combination.

Since the voltage adds up, we can find the amount of voltage across the 3pF capacitor with the remaining going through the branches of the parallel combination.

`V = (Q)/(C)\\\\V = (9pC)/(3pF) = 3V`

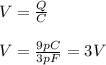
Therefore, 3V goes through each branch since 6V - 3V = 3V.

Solving for the charge for each capacitor:

`Q = CV\\Q = (1 pF)(3V) = 3pC\\\\Q = (2pF)(3V) = 6pC\\\\Q = (3pF)(3V) = 9pC`

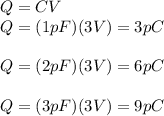
Thus, the capacitor with the greatest charge is the 3 pF capacitor.

To explain without all of the work above, the equivalent capacitance of the parallel combination (1 pF + 2pF = 3pF) is equivalent to the capacitance of the capacitor in series (3pF). Thus, the voltage across the parallel capacitors (since voltage is the same across branches in parallel) and the series capacitor is equal. However, since charge SUMS UP for capacitors in parallel, they would have less charge than the single capacitor in series.