Question

Rectangle ABCD is dilated with center at (0, 0) and scale factor 2. Select the three statements that are true about the dilation.

Answer 1

well im confused but dont you have to find the prime too

Explanation:

Answer 2

Options (3), (4) and (6)

Explanation:

Coordinates of the vertices of the given rectangle are,

A(1, 5), B(3, 2), C(-3, -2) and D(-5, 1)

When rectangle ABCD is dilated by a scale factor of 2 about the origin,

Rule to be followed for the dilation,

(x, y) → (2x, 2y)

Therefore, image of the rectangle ABCD will be,

A(1, 5) → A'(2, 10)

B(3, 2) → B'(6, 4)

C(-3, -2) → C'(-6, -4)

D(-5, 1) → D'(-10, 2)

- Hence point B' is located at (6, 4).

- Rectangle ABCD and A'B'C'D' are similar as all the angles of image will be same as the pre-image after rigid transformation (dilation).

- Let the equation of the line B'C' is,

y = mx + b

Slope (m) =
`(y_2-y_1)/(x_2-x_1)`

=
`(4-2)/(6-3)`

=
`(2)/(3)`

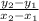
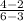
Since B'C' will pass through origin, y-intercept will be zero.

Therefore, equation of B'C' will be,

y =
`(2)/(3)x`

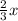
Options (3), (4) and (6) are the correct options.