Question

Una barca intenta cruzar un río. La barca lleva una velocidad de 3 m/s con dirección perpendicular a la de la velocidad del agua que es de 4 m/s. Si el ancho del río es de 120 m. El tiempo en llegar a la otra orilla es de:

Answer 1

El tiempo que tarda la barca en llegar a la orilla es 40 s.

Step-by-step explanation:

Debido a que el río se mueve en dirección perpendicular a la barca, ésta se va a mover de manera diagonal, cuya velocidad (
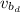`v_{b_(d)}`) viene dada por:

`|v_{b_(d)}| = \sqrt{v_(r)^(2) + v_(b)^(2)} = \sqrt{(4)^(2) + (3)^(2)} = 5 m/s`

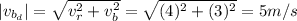
Por lo tanto, el módulo del vector velocidad diagonal es 5 m/s, y su dirección es:

`tan(\alpha) = (v_(r))/(v_(b)) = (4)/(3)`

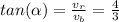
Entonces, α es:

`\alpha = arctan((4)/(3)) = 53.13 ^(\circ)`

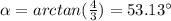
Ahora, debemos encontrar la distancia de la longitud diagonal que recorre la barca:

`cos(\alpha) = (a)/(d_(d))`

`d_(d) = (a)/(cos(\alpha)) = (120 m)/(cos(53.13)) = 200.0 m`

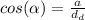
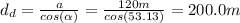
Finalmente, el tiempo que le tomaría a la barca recorrer 200 m sería:

`v_{b_(d)} = (d_(d))/(t)`

`t = (200 m)/(5 m/s) = 40 s`

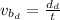
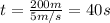
Por lo tanto, el tiempo que tarda la barca en llegar a la orilla es 40 s.

Espero que te sea de utilidad!