Question

There are 3 islands A,B,C. Island B is east of island A, 8 miles away. Island C is northeast of A, 5 miles away and northwest of B, 7 miles away. What is the bearing needed to navigate from island B to C? Round to the nearest degree

Answer 1

The bearing needed to navigate from island B to island C is approximately 38.213º.

Explanation:

The geometrical diagram representing the statement is introduced below as attachment, and from Trigonometry we determine that bearing needed to navigate from island B to C by the Cosine Law:

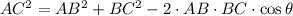`AC^(2) = AB^(2)+BC^(2)-2\cdot AB\cdot BC\cdot \cos \theta` (1)

Where:

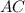`AC` - The distance from A to C, measured in miles.

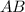`AB` - The distance from A to B, measured in miles.

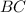`BC` - The distance from B to C, measured in miles.

`\theta` - Bearing from island B to island C, measured in sexagesimal degrees.

Then, we clear the bearing angle within the equation:

`AC^(2)-AB^(2)-BC^(2)=-2\cdot AB\cdot BC\cdot \cos \theta`

`\cos \theta = (BC^(2)+AB^(2)-AC^(2))/(2\cdot AB\cdot BC)`

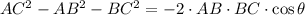
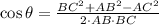
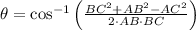`\theta = \cos^(-1)\left((BC^(2)+AB^(2)-AC^(2))/(2\cdot AB\cdot BC) \right)` (2)

If we know that
`BC = 7\,mi`,
`AB = 8\,mi`,
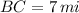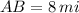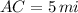`AC = 5\,mi`, then the bearing from island B to island C:

`\theta = \cos^(-1)\left[((7\mi)^(2)+(8\,mi)^(2)-(5\,mi)^(2))/(2\cdot (8\,mi)\cdot (7\,mi)) \right]`

`\theta \approx 38.213^(\circ)`

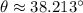
The bearing needed to navigate from island B to island C is approximately 38.213º.