Answer:
Approximately
 , assuming that the gravitational field strength is
, assuming that the gravitational field strength is
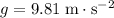 .
.
Step-by-step explanation:
Let
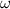 denote the required angular velocity of this Ferris wheel. Let
denote the required angular velocity of this Ferris wheel. Let
 denote the mass of a particular passenger on this Ferris wheel.
denote the mass of a particular passenger on this Ferris wheel.
At the topmost point of the Ferris wheel, there would be at most two forces acting on this passenger:
- Weight of the passenger (downwards),
 , and possibly
, and possibly - Normal force
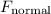 that the Ferris wheel exerts on this passenger (upwards.)
that the Ferris wheel exerts on this passenger (upwards.)
This passenger would feel "weightless" if the normal force on them is
 - that is,
- that is,
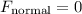 .
.
The net force on this passenger is
 . Hence, when
. Hence, when
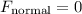 , the net force on this passenger would be equal to
, the net force on this passenger would be equal to
 .
.
Passengers on this Ferris wheel are in a centripetal motion of angular velocity
 around a circle of radius
around a circle of radius
 . Thus, the centripetal acceleration of these passengers would be
. Thus, the centripetal acceleration of these passengers would be
 . The net force on a passenger of mass
. The net force on a passenger of mass
 would be
would be
 .
.
Notice that
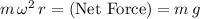 . Solve this equation for
. Solve this equation for
 , the angular speed of this Ferris wheel. Since
, the angular speed of this Ferris wheel. Since
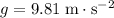 and
and
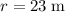 :
:
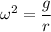 .
.
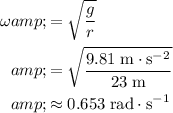 .
.
The question is asking for the angular velocity of this Ferris wheel in the unit
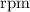 , where
, where
 . Apply unit conversion:
. Apply unit conversion:
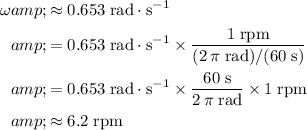 .
.