Answer:
The speed of the water flow in the pipe on the second floor is approximately 13.1 meters per second.
Step-by-step explanation:
By assuming that fluid is incompressible and there are no heat and work interaction through the line of current corresponding to the pipe, we can calculate the speed of the water floor in the pipe on the second floor by Bernoulli's Principle, whose model is:
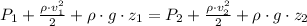 (1)
(1)
Where:
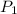 ,
,
 - Pressures of the water on the first and second floors, measured in pascals.
- Pressures of the water on the first and second floors, measured in pascals.
 - Density of water, measured in kilograms per cubic meter.
- Density of water, measured in kilograms per cubic meter.
 ,
,
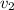 - Speed of the water on the first and second floors, measured in meters per second.
- Speed of the water on the first and second floors, measured in meters per second.
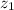 ,
,
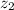 - Heights of the water on the first and second floors, measured in meters.
- Heights of the water on the first and second floors, measured in meters.
Now we clear the final speed of the water flow:
![(\rho\cdot v_(2)^(2))/(2) = P_(1)-P_(2)+\rho \cdot \left[(v_(1)^(2))/(2)+g\cdot (z_(1)-z_(2)) \right]](https://img.qammunity.org/2021/formulas/physics/high-school/t0byb9xwskbfmrhkvmfz00yxfsu2e2pvwp.png)
![\rho\cdot v_(2)^(2) = 2\cdot (P_(1)-P_(2))+\rho\cdot [v_(1)^(2)+2\cdot g\cdot (z_(1)-z_(2))]](https://img.qammunity.org/2021/formulas/physics/high-school/l0jylz5vj1soqjlowsx6myccyrc2itwvae.png)
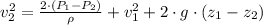
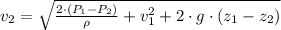 (2)
(2)
If we know that
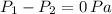 ,
,
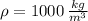 ,
,
 ,
,
 and
and
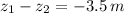 , then the speed of the water flow in the pipe on the second floor is:
, then the speed of the water flow in the pipe on the second floor is:
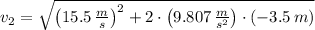
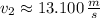
The speed of the water flow in the pipe on the second floor is approximately 13.1 meters per second.