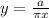Question

The area, LaTeX: aa, of an ellipse can be determined using the formula LaTeX: a=\pi xya = π x y, where LaTeX: xx and LaTeX: yy are half the lengths of the largest and smallest diameters of the ellipse. Which is an equivalent equation solved for LaTeX: yy? Group of answer choices LaTeX: y=a-\pi x y = a − π x LaTeX: y=a\ast \pi x y = a ∗ π x LaTeX: y=a\div (\pi x) y = a ÷ ( π x ) LaTeX: y=a+(\pi x)

Answer LaTeX: y=a\div (\pi x)y = a ÷ ( π x )

Answer 1

Question:

The area, a, of an ellipse can be determined using the formula a = πxy, where x and y are half the lengths of the largest and smallest diameters of the ellipse. Which is an equivalent equation solved for y?

Answer:

`y = (a)/(\pi x)`

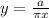
Explanation:

Given

`a = \pi xy`

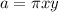
Required

Solve for y

The question implies that, we make y the subject of formula:

This is done as follows:

`a = \pi xy`

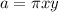
Divide through by
`\pi x`

`(a)/(\pi x) = (\pi xy)/(\pi x)`

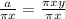
Isolate y on the right hand side

`(a)/(\pi x) = y`

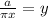
Reorder

`y = (a)/(\pi x)`

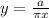
Hence, the solution to the question is:
`y = (a)/(\pi x)`