Question

At a festival, spherical balloons with a radius of

110.cm


are to be inflated with hot air and released. The air at the festival will have a temperature of


25°C


and must be heated to


100°C


to make the balloons float.


3.00kg


of butane


C4H10


fuel are available to be burned to heat the air. Calculate the maximum number of balloons that can be inflated with hot air.


Here are some data you may find useful:


Specific heat capacity of air:

1.009J·g°C


Density of air at

100°C


:

0.946kgm3


Density of butane at

100°C


:

1.898kgm3


Formation enthalpy of butane at

25°C


:

Answer 1

100C because he inflated the hot air balloon

Answer 2

The maximum number of balloons that can be inflated with the available fuel and conditions is approximately 3.9.

How to find maximum number?

Balloon radius (r) = 110 cm (convert to m later)

Initial air temperature (
`T_i`) = 25°C + 273.15 K

= 298.15 K

Final air temperature (
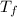`T_f`) = 100°C + 273.15 K

= 373.15 K

Density of air at final temperature (
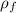`\rho_f`) = 0.946 kg/m³

Butane mass (
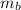`m_b`) = 3.00 kg

Specific heat capacity of air (
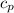`c_p`) = 1.009 J/g°C (convert to J/kg°C later)

Formation enthalpy of butane (
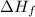`\Delta H_f`) = -2878.4 kJ/mol

Calculate balloon volume:

Volume of a sphere = (4/3)πr³

Balloon volume (
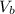`V_b`) = (4/3)π × (1.1 m)³

≈ 5.24 m³

Calculate air mass required per balloon:

`\text {Air mass} (m_a) = \rho_f * V_b`

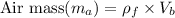
= 0.946 kg/m³ × 5.24 m³

≈ 4.95 kg

Calculate temperature difference required per balloon:

`\Delta T = T_f - T_i`

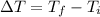
= 373.15 K - 298.15 K

= 75 K

Calculate heat required per balloon:

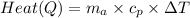`Heat (Q) = m_a * c_p * \Delta T` (convert
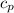`c_p` to J/kg°C first)

Q = 4.95 kg × 1009 J/(kg°C) × 75 K

Q ≈ 371452.5 J

Calculate moles of butane burned per balloon:

Moles of butane (
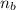`n_b`) = Q / (
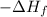`-\Delta H_f`) (convert
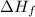`\Delta H_f` to J/mol first)

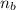`n_b` = 371452.5 J / (-2878400 J/mol)

≈ 0.013 mol

Calculate number of balloons possible:

Total moles of butane (n_b_total) =
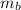`m_b` / (molar mass of butane)

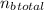`n_b_{total` = 3.00 kg / 58.12 g/mol

≈ 0.051 mol

`\text {Number of balloons} = (n_b_(total))/(n_b )`

≈ 3.9

Therefore, the maximum number of balloons that can be inflated with the available fuel and conditions is approximately 3.9.