Question

What if the frequency is now increased to f = 69 Hz, and we want to keep the impedance unchanged? (A) What new resistance should we use to achieve this goal? R = Ω (B) What is the phase angle (in degrees) between the current and the voltage now? ϕ = ° (C) Find the maximum voltages across each element.

Answer 1

Complete Question

A series RLC circuit has R = 405 Ω, L = 1.40 H, C = 3 µF. It is connected to an AC source with f = 60.0 Hz and ΔVmax = 150 V. What if the frequency is now increased to f = 69 Hz, and we want to keep the impedance unchanged? (A) What new resistance should we use to achieve this goal? R = Ω (B) What is the phase angle (in degrees) between the current and the voltage now? ϕ = ° (C) Find the maximum voltages across each element.

Answer:

A

`R = 513.9 \ \Omega`

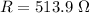
B

`\theta = 34.79^o`

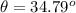
C

`V_c =212.96 \ V` ,
`V_L = 168.139 \ V` ,
`V_R = 142.35 \ V`

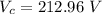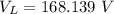Step-by-step explanation:

From the question we are told that

The resistance is
`R = 405 \ \Omega`

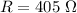
The inductance is L = 1.40 H

The capacitance is
`C = 3 \mu F = 3 *10^(-6) \ F`

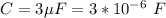
The original frequency is
`f = 60 \ Hz`

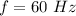
The new frequency is
`f_1 = 69 \ Hz`

Generally the reactance of the inductor is mathematically represented as

`X_L = 2 \pi * f * L`

=>
`X_L = 2 * 3.142 * 60 * 1.40`

=>
`X_L = 527.5 \ \Omega`

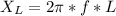
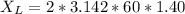
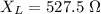
Generally the reactance of the capacitor is mathematically represented as

`X_c = (1)/(2 \pi * f * C)`

`X_c = (1)/(2 * 3.142 * 60 * 3*10^(-6))`

=>
`X_c = 884.6 \ \Omega`

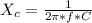
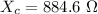
Generally the impedance of the circuit is mathematically represented as

`Z = √([X_L - X_c ]^2 + R^2)`

=>
`Z = √([527.5 -884.6 ]^2 + 405^2)`

=>
`Z = 540 \ \Omega`

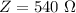
Generally when the frequency is changed , the reactance of the inductor becomes

`X_L' = 2 * 3.142 * 69 * 1.4`

=>
`X_L' = 607 \ \Omega`

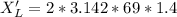
Generally when the frequency is changed , the reactance of the capacitor becomes

`X_c' = (1)/(2 * 3.142 * 69 * 3*10^(-6))`

=>
`X_c ' = 768.8 \ \Omega`

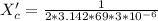
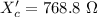
Generally the new resistance is mathematically represented as

`R ^2 = Z^2 - ( X_c' - X_L')^2`

=>
`R ^2 = 540^2 - ( 603 - 768.8 )^2`

=>
`R = √(264110.4)`

=>
`R = 513.9 \ \Omega`

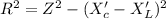
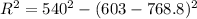
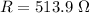
Generally the phase angle is mathematically represented as

`\theta = tan^(-1)[([X_L - X_C])/(R) ]`

=>
`\theta = tan^(-1)[([ 884.6 - 527.5])/(513.92) ]`

=>
`\theta = 34.79^o`

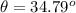
Generally the maximum current flowing through the circuit is mathematically represented as

`I_(max) = (\Delta V)/( Z)`

=>
`I_(max) = (150)/(540 )`

=>
`I_(max) = 0.2778 \ A`

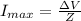
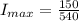
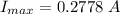
Generally the maximum voltage across the capacitor is

`V_c = I_(max) * X_c'`

`V_c = 0.2778* 768.8`

=>
`V_c =212.96 \ V`

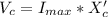
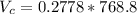
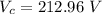
Generally the maximum voltage across the inductor is

`V_L = I_(max) * X_L`

`V_L = 0.2778* 607`

=>
`V_L = 168.139 \ V`

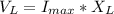
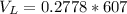
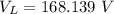
Generally the maximum voltage across the resistor is

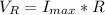
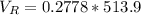
`V_R = I_(max) * R`

`V_R = 0.2778* 513.9`

=>
`V_R = 142.35 \ V`