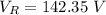Complete Question
A series RLC circuit has R = 405 Ω, L = 1.40 H, C = 3 µF. It is connected to an AC source with f = 60.0 Hz and ΔVmax = 150 V. What if the frequency is now increased to f = 69 Hz, and we want to keep the impedance unchanged? (A) What new resistance should we use to achieve this goal? R = Ω (B) What is the phase angle (in degrees) between the current and the voltage now? ϕ = ° (C) Find the maximum voltages across each element.
Answer:
A
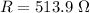
B
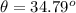
C
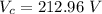 ,
,
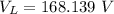 ,
,
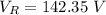
Step-by-step explanation:
From the question we are told that
The resistance is
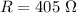
The inductance is L = 1.40 H
The capacitance is
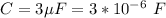
The original frequency is
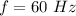
The new frequency is
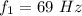
Generally the reactance of the inductor is mathematically represented as
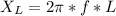
=>
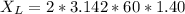
=>
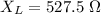
Generally the reactance of the capacitor is mathematically represented as
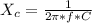
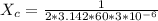
=>
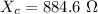
Generally the impedance of the circuit is mathematically represented as
![Z = √([X_L - X_c ]^2 + R^2)](https://img.qammunity.org/2021/formulas/physics/high-school/2wfj3akjqyxnhrtdo1sfwdug96wh4qyg4w.png)
=>
![Z = √([527.5 -884.6 ]^2 + 405^2)](https://img.qammunity.org/2021/formulas/physics/high-school/f4y0e4ty9dzkrt6tlxu5h19pb6tnyvkf35.png)
=>
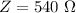
Generally when the frequency is changed , the reactance of the inductor becomes
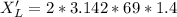
=>
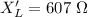
Generally when the frequency is changed , the reactance of the capacitor becomes
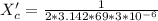
=>
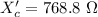
Generally the new resistance is mathematically represented as
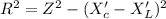
=>
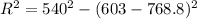
=>
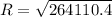
=>
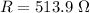
Generally the phase angle is mathematically represented as
![\theta = tan^(-1)[([X_L - X_C])/(R) ]](https://img.qammunity.org/2021/formulas/physics/high-school/3nebd4eygtq2biboyjg8vvaz3ak9cuz1wq.png)
=>
![\theta = tan^(-1)[([ 884.6 - 527.5])/(513.92) ]](https://img.qammunity.org/2021/formulas/physics/high-school/vpcd2a51x4o9tzt5bfz88dwb5zbpzhrk67.png)
=>
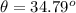
Generally the maximum current flowing through the circuit is mathematically represented as
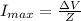
=>
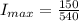
=>
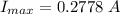
Generally the maximum voltage across the capacitor is
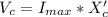
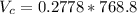
=>
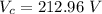
Generally the maximum voltage across the inductor is
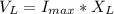
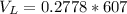
=>
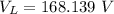
Generally the maximum voltage across the resistor is
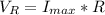
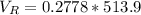
=>