Answer:
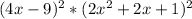
Explanation:
(((4x-9)•(((2•(x2))+2x)+1))•(4x-9))•((2x2+2x)+1)
] (((4x-9)•((2x2+2x)+1))•(4x-9))•(2x2+2x+1)
Trying to factor by splitting the middle term
Factoring 2x2+2x+1
The first term is, 2x2 its coefficient is 2 .
The middle term is, +2x its coefficient is 2 .
The last term, "the constant", is +1
Step-1 : Multiply the coefficient of the first term by the constant 2 • 1 = 2
Step-2 : Find two factors of 2 whose sum equals the coefficient of the middle term, which is 2 .
-2 + -1 = -3
-1 + -2 = -3
1 + 2 = 3
2 + 1 = 3
Observation : No two such factors can be found !!
Conclusion : Trinomial can not be factored
((4x-9)•(2x2+2x+1)•(4x-9))•(2x2+2x+1)
Multiplying Exponential Expressions:
4.1 Multiply (4x-9) by (4x-9)
The rule says : To multiply exponential expressions which have the same base, add up their exponents.
In our case, the common base is (4x-9) and the exponents are :
1 , as (4x-9) is the same number as (4x-9)1
and 1 , as (4x-9) is the same number as (4x-9)1
The product is therefore, (4x-9)(1+1) = (4x-9)2
Trying to factor by splitting the middle term
5.1 Factoring 2x2+2x+1
The first term is, 2x2 its coefficient is 2 .
The middle term is, +2x its coefficient is 2 .
The last term, "the constant", is +1
Step-1 : Multiply the coefficient of the first term by the constant 2 • 1 = 2
Step-2 : Find two factors of 2 whose sum equals the coefficient of the middle term, which is 2 .
-2 + -1 = -3
-1 + -2 = -3
1 + 2 = 3
2 + 1 = 3
Observation : No two such factors can be found !!
Conclusion : Trinomial can not be factored
Multiplying Exponential Expressions:
5.2 Multiply (2x2+2x+1) by (2x2+2x+1)
The rule says : To multiply exponential expressions which have the same base, add up their exponents.
In our case, the common base is (2x2+2x+1) and the exponents are :
1 , as (2x2+2x+1) is the same number as (2x2+2x+1)1
and 1 , as (2x2+2x+1) is the same number as (2x2+2x+1)1
The product is therefore, (2x2+2x+1)(1+1) = (2x2+2x+1)2
Final result :
(4x - 9)2 • (2x2 + 2x + 1)2