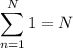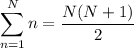Question

Find the sum of the first 100
terms of the arithmetic
sequence.
a₁ 15 and a100=307

Answer 1

The sequence is arithmetic, so there is a constant difference d between consecutive terms such that

`a_(100) = a_(99) + d`

`a_(100) = (a_(98) + d) + d = a_(98) + 2d`

`a_(100) = (a_(97) + d) + 2d = a_(97) + 3d`

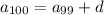
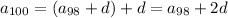
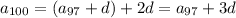
and so on, down to

`a_(100) = a_1 + 99d`

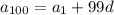
(notice the pattern of 100 = 99 + 1 = 98 + 2 = 97 + 3 = … = 1 + 99)

Solve for d :

`307 = 15 + 99d \implies 99d = 292 \implies d = (292)/(99)`

Now, the sum of the first 100 terms of this sequence is

`\displaystyle \sum_(n=1)^(100) a_n = \sum_(n=1)^(100) \left(15 + (292)/(99)(n-1)\right) = \boxed{16100}`

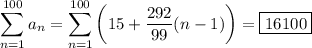
which follows from the well-known sums

`\displaystyle \sum_(n=1)^N 1 = N`

`\displaystyle \sum_(n=1)^N n = \frac{N(N+1)}2`